(潍坊爱普环保设备有限公司)
摘 要 本文主要通过自由淹没射流理论研究除尘器设计的相关课题。
关键词 自由射流 喷管 扩张角
1 自由淹没射流的基本流动特性
一股速度很大的流动射入周围流体时所形成的流动,称之为射流。射流周围的流体本身具有速度时称为伴随射流,当周围流体处于静止状态时,则称为自由射流。射流将一部分动量传递给带入的流体,因而射流的速度逐渐降低。最后射流的动量全部消失在空间流体中,射流也在静止流体中淹没了,所以又称它为自由淹没射流。
射流一般分为初始段和基本段两部分。图1所示为自由射流的结构示意图。
假定流体以超过临界速度的初速度U0均匀地从喷管出口流出,在流动中由于周围流体的不断掺入,射流的宽度逐渐增大,而在射流中还保持射流初速U0的区域(称为射流核心区)则逐渐缩小。在离开喷管出口一定距离以后,保持初速U0的射流核心区就消失了。射流核心区完全消失的横截面称为转折截面。在喷管出口与转折截面之间的射流段称为初始段,射流核心区就在初始段中。在转折截面以后的射流段称为基本段,在基本段中轴向流速逐渐减小,最后到零。射流与静止流体的交界面(流速为零)称为外边界面,轴向流速还保持初速U0的边界面(射流核心区的边界面)称为内边界面。在内、外边界面之间的区域称为射流边界层,在转折截面以后整个射流都变成射流边界层。射流外边界现的交点O称为射流极点,它的位置在喷管内。外边界线之间的夹角θ称为射流极角,也称为射流扩散角。
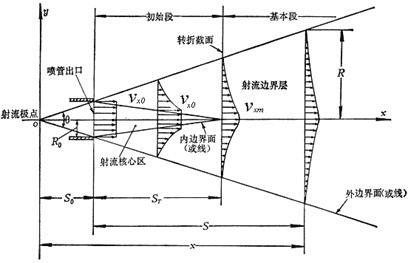
图1 自由射流的结构示意图
剪切射流符合边界层的特点:射流边界层的宽度小于射流的长度,即横向尺度远小于纵向尺度;在射流边界层的任何横截面上,横向速度远小于纵向速度;沿射流边界层横截面上的压强是近似不变的,又由于周围静止流体内的压强各处都相等,所以可以认为,整个射流区内的压强都是一样的;射流边界层的内、外边界线都是直线。
根据自由淹没射流理论,圆形截面轴向对称射流有以下特征:
转折截面上射流宽度等于喷管出口直径的3.28倍。
射流扩散角θ为270-30030'
射出能力Um=U0*0.966/(α*S/R0+0.294) α=0.07-0.08
2 自由淹没射流理论在脉冲喷吹设计中的应用
脉冲喷吹滤袋除尘器在设计过程中,常常涉及喷管设计。喷管设计主要包括喷管形式、喷口大小、喷口高度。
喷管外表形式多种多样,究其根本只有两种:收缩喷管、缩放喷管。收缩喷管的流通截面是逐渐缩小的,流通截面不变的喷管本质上也属于收缩喷管。缩放喷管的流通截面是先缩小后扩大。缩放喷管也称拉伐尔喷管。亚音速气流在收缩喷管内膨胀加速,不可能得到超音速流动。要得到超音速流动,必须在渐缩渐扩形的拉伐尔喷管内才能得到超音速流动。
由于当前脉冲滤袋除尘领域并未涉及超音速喷吹清灰,下面仅以收缩喷管为例进行研究。
高速压缩空气通过喷管对滤袋进行喷吹清灰,其速度可以达到接近临界音速。临界音速不是一个定值,与温度有关。在0℃时,空气的临界音速为302m/s。也就是说,在普通喷管的喷口0℃时最大速度为接近302m/s。而滤袋上口净气流出速度一般不大于5m/s,相对于喷吹气流可以暂时忽略。这样,可以利用自由淹没射流理论对喷管高度进行计算。
以φ160滤袋(笼口φ150)、喷口φ20,φ130滤袋(笼口φ120)喷口φ10为例如图2说明:
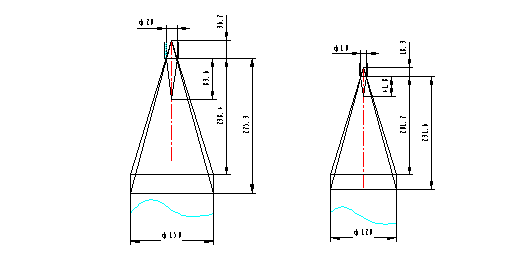
图2 φ160和φ130滤袋喷射情况
由射流扩散角θ为270-30030',很容易计算出笼口φ150、喷口φ20时的喷吹高度在238.4-275.3之间。理论上,如果高于此高度,即有部分空气吹到多孔板外面造成浪费。如果低于此高度,可能会造成滤袋顶部清灰不利。在实践应用当中,因为喷管安装偏离等其它方面原因,实际高度一般会略低于此高度。同理,可以计算出笼口φ120、喷口φ10时的喷吹高度在201.7-231.6之间。
根据公式Um=U0*0.966/(α*S/R0+0.294),可以计算袋口喷吹气流的理论速度:
表1 袋口喷吹气流的理论速度
|
条件:喷口速度接近302 m/s |
袋口气流速度(m/s) |
|
笼口φ150、喷口φ20、喷吹高度230 |
约144.5 |
|
笼口φ120、喷口φ10、喷吹高度200 |
约88.5 |
因为受到袋口净气上升速度影响,实际速度要略小于理论计算速度。
喷吹气体进入滤袋以后,气体受到滤袋周壁的约束,不能继续扩散,所以不再适用于自由淹没射流理论进行研究。
3 自由淹没射流理论在直通式滤袋除尘器进风口设计中的分析研究
在直通式滤袋除尘器设计时,进风口后滤袋迎风面受风速度要求严格,如果不能得到有效控制,很容易吹损滤袋。利用自由淹没射流理论同样可以分析进风口相关部位的风速结构。
以φ1000进风管道为例进行分析。如图3,进风管道连接喇叭形进风口。
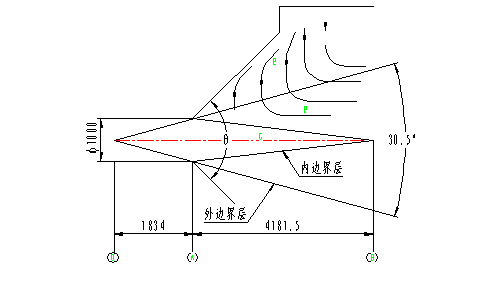
图3 进风管喇叭形连接
气流以管道风速U0均匀地从管口(A)流出,进入喇叭口(扩张角θ)。由于流通面积不断扩大,在流动中周围流体不断掺入,射流的宽度逐渐增大,而在射流中还保持射流初速U0的区域则逐渐缩小。在离开喷管出口一定距离(4181.5)以后,保持初速U0的射流核心区就消失了。
现在讨论两种情况,喇叭口扩张角θ>30.50时(不是定值,介于27-30.50之间,为简化分析以30.50为例,下同),如上图所示。由于周围流体要不断掺入,而喇叭周壁阻挡了上下两个方向上的气流,所以只能由喇叭后端补充,从而在喇叭口周围形成涡流,产生能量损失。如图,E区为涡流区,速度为负值;F区流速介于零到管道风速之间;G区流速与管道风速相同。
由上分析可知,在喇叭口末端的流速,是不均匀的,单纯用流量除以截面积所得理论平均流速并无实践意义。要想得到均匀的流体速度,有两个措施:一是将喇叭口做长,可以得到相对均匀设计流速。这种措施在实践中也有应用,并非运用于直通式袋除尘器。另一种措施是加均风板,用外力减弱流体前进速度,强制补充涡流区,这种措施已经得到广泛应用。
另一种情况是当喇叭口扩张角θ<30.50时,射流自动充满喇叭空间,周围静止流体由于受到喇叭周壁的阻挡,不会有流体掺入,所以没有涡流。这种情况不再属于自由淹没射流理论的研究范围,而属于亚音速扩压管研究的范围,其特征是随着气流的截面积增大,流速减小,压力增大。其均风效果更有效。
所以说,在不设均风板时,喇叭口的扩张角如果高于300,是不科学的。
自由淹没射流理论在其它地方也可以应用,譬如可以对滤袋出口的净气流速进行分析,分析某高度点的气体速度,可以为净气室的高度设计提供理论依据。在除尘系统设计中,也有一些地方可以利用该理论进行分析研究。
选自2009全国袋式除尘技术研讨会论文集 | 
